Кинетическая и потенция энергия

Энергия – важнейшее понятие в механике. Что такое энергия. Существует множество определений, и вот одно из них.
Что такое энергия?
Энергия – это способность тела совершать работу.
Кинетическая энергия
Рассмотрим тело, которое двигалось под действием каких-то сил изменило свою скорость с v1→ до v2→. В этом случае силы, действующие на тело, совершили определенную работу A.
Работа всех сил, действующих на тело, равна работе равнодействующей силы.
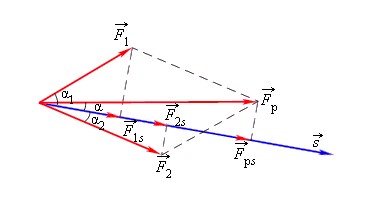
Fр→=F1→+F2→
A=F1·s·cosα1+F2·s·cosα2=Fрcosα.
Установим связь между изменением скорости тела и работой, совершенной действующими на тело силами. Для простоты будем считать, что на тело действует одна сила F→, направленная вдоль прямой линии. Под действием этой силы тело движется равноускоренно и прямолинейно. В этом случае векторы F→, v→, a→, s→ совпадают по направлению и их можно рассматривать как алгебраические величины.
Работа силы F→ равна A=Fs. Перемещение тела выражается формулой s=v22-v122a. Отсюда:
A=Fs=F·v22-v122a=ma·v22-v122a
A=mv22-mv122=mv222-mv122.
Как видим, работа, совершенная силой, пропорционально изменению квадрата скорости тела.
Определение. Кинетическая энергия
Кинетическая энергия тела равна половине произведения массы тела на квадрат его скорости.
EK=mv22.
Кинетическая энергия – энергия движения тела. При нулевой скорости она равна нулю.
Теорема о кинетической энергии
Вновь обратимся к рассмотренному примеру и сформулируем теорему о кинетической энергии тела.
Теорема о кинетической энергии
Работа приложенной к телу силы равна изменению кинетической энергии тела. Данное утверждение справедливо и тогда, когда тело движется под действием изменяющейся по модулю и направлению силы.
A=EK2-EK1.
Таким образом, кинетическая энергия тела массы m, движущегося со скоростью v→, равна работе, которую сила должна совершить, чтобы разогнать тело до этой скорости.
A=mv22=EK.
Чтобы остановить тело, нужно совершить работу
A=-mv22=-EK
Потенциальная энергия
Кинетическая энергия – это энергия движения. Наряду с кинетической энергией есть еще потенциальная энергия, то есть энергия взаимодействия тел, которая зависит от их положения.
Например, тело поднято над поверхностью земли. Чем выше оно поднято, тем больше будет потенциальная энергия. Когда тело падает вниз под действием силы тяжести, эта сила совершает работу. Причем работа силы тяжести определяется только вертикальным перемещением тела и не зависит от траектории.
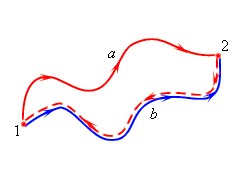
Важно!
Вообще о потенциальной энергии можно говорить только в контексте тех сил, работа которых не зависит от формы траектории тела. Такие силы называются консервативными.
Примеры консервативных сил: сила тяжести, сила упругости.
Когда тело движется вертикально вверх, сила тяжести совершает отрицательную работу.
Рассмотрим пример, когда шар переместился из точки с высотой h1 в точку с высотой h2.
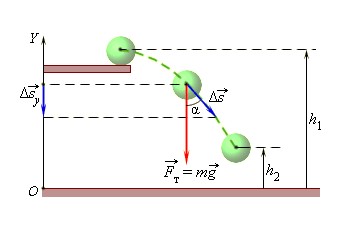
При этом сила тяжести совершила работу, равную
A=-mg(h2-h1)=-(mgh2-mgh1).
Эта работа равна изменению величины mgh, взятому с противоположным знаком.
Величина ЕП=mgh – потенциальна энергия в поле силы тяжести. На нулевом уровне (на земле) потенциальная энергия тела равна нулю.
Определение. Потенциальная энергия
Потенциальная энергия – часть полной механической энергии системы, находящейся в поле консервативных сил. Потенциальная энергия зависит от положения точек, составляющих систему.
Можно говорить о потенциальной энергии в поле силы тяжести, потенциальной энергии сжатой пружины и т.д.
Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.
A=-(EП2-EП1).
Ясно, что потенциальная энергия зависит от выбора нулевого уровня (начала координат оси OY). Подчеркнем, что физический смысл имеет изменение потенциальной энергии при перемещении тел друг относительно друга. При любом выборе нулевого уровня изменение потенциальной энергии будет одинаковым.
При расчете движения тел в поле гравитации Земли, но на значительных расстояниях от нее, во внимание нужно принимать закон всемирного тяготения (зависимость силы тяготения от расстояния до цента Земли). Приведем формулу, выражающую зависимость потенциальной энергии тела.
EП=-GmMr.
Здесь G – гравитационная постоянная, M – масса Земли.
Потенциальная энергия пружины
Представим, что в первом случае мы взяли пружину и удлинили ее на величину x. Во втором случае мы сначала удлинили пружину на 2x, а затем уменьшили на x. В обоих случаях пружина оказалась растянута на x, но это было сделано разными способами.
При этом работа силы упругости при изменении длины пружины на x в обоих случаях была одинакова и равна
Aупр=-A=-kx22.
Величина Eупр=kx22 называется потенциальной энергией сжатой пружины. Она равна работе силы упругости при переходе из данного состояния тела в состояние с нулевой деформацией.
Источник
Анастасия Еремина
22 апреля 2016 · 124,2 K
Кинетическая энергия – это энергия движения тела. Соотвественно, если у нас есть какой-то объект, обладающий хоть какой-то массой и хоть какой-то скоростью, то он и обладает кинетической энергией. Однако относительно разных систем отсчета эта кинетическая энергия у одного и того же объекта может быть разной.
Пример. Есть бабушка, которая относительно земли нашей планеты находится в состоянии покоя, то есть не движется и, скажем, сидит на остановке в ожидании своего автобуса. Тогда относительно нашей планеты ее кинетическая энергия равна нулю. Но если посмотреть на эту же бабушку с Луны или с Солнца, относительно которых можно наблюдать движение планеты и, соответственно, этой бабушки, которая находится на нашей планете, то бабушка уже будет обладать кинетической энергией относительно упомянутых небесных тел. И тут приезжает автобус. Эта самая бабушка быстро встает и бежит занимать положенное ей место. Теперь относительно планеты она уже не в покое, а вполне себе движется. А значит и обладает кинетической энергией. И чем толще бабушка и быстрее, тем больше ее кинетическая энергия.
Есть несколько фундаментальных видов энергии – основных. Расскажу, например, про механические. К ним относятся энергия кинетическая, которая зависит от скорости и массы объекта, энергия потенциальная, которая зависит от того, где вы возьмете нулевой уровень потенциальной энергии, и от того положения, где находится этот объект относительно нулевого уровня потенциальной энергии. То есть потенциальная энергия – энергия, зависящая от положения объекта. Эта энергия характеризует работу, совершаемую полем, в котором находится объект, по его перемещению.
Пример. Несете вы в руках огромную коробку и падаете. Коробка лежит на полу. Выходит, что нулевой уровень потенциальной энергии у вас будет находится, соответственно, на уровне пола. Тогда верхняя часть коробки будет обладать большей потенциальной энергией, так как она находится выше пола и выше нулевого уровня потенциальной энергии.
Глупо говорить про энергию, не упомянув закон о ее сохранении. Таким образом, по закону сохранения энергии, эти два ее вида, описывающих состояние объекта, ни откуда не берутся и никуда не исчезают, а только переходят друг в друга.
А вот и пример. Падаю я с высоты дома, изначально имея потенциальную энергию относительно земли в момент перед прыжком, а моя кинетическая энергия пренебрежимо мала, поэтому можем приравнять её к нулю. Вот я отрываю ножки от карниза и моя потенциальная энергия начинает уменьшаться, так как высота, на которой я нахожусь, становится все меньше и меньше. В этот же момент при падении вниз я постепенно приобретаю кинетическую энергию, так как падаю вниз все с большей скоростью. В момент падения я уже обладаю максимальной кинетической энергией, но потенциальная равно нулю, такие дела.
Спасибо, очень просто и понятно.
Энергия – это в первую очередь величина, характеризующая возможность тела совершить работу.
Кинетическая энергия – это энергия движения тела. Простейший пример – пуля. Пуля какой-то массы летит с какой – то скоростью. Врезавшись в какое – либо твердое тело она сдвинет его (или, возможно, пробьет) с большей вероятностью в том случае, если у нее больше… Читать далее
Судя по названию, кинетическая – это энергия движения, а потенциальная – энергия, которую тело может иметь. На самом деле кинетическая – это действиельно энергия движения, а потенциальная – это вообще энергия связи в системе. Конкретно потенциальная механическая – это энергия гравитационного звимодействия дух тел между собой. Выделяться способны обе.
Энергия — это нечто, что сохраняется.
Это самое важное, что нужно о ней понимать. Учёные хотели объяснить, что, например, качающийся маятник не может без постороннего вмешательства начать качаться сильнее (то есть, что его энергия не может сама увеличиться). Для этого ввели понятие энергии.
Пусть, например, относительно одной системы отсчёта у меня… Читать далее
Что такое закон сохранения энергии?
Всем, привет! Тема семьи и отношений очень близка мне, но, став мамой, нужно…
Данный закон один из фундаментов законов природы. Основная суть ео в том, что в замкнутой ситеме энергия никуда не теряется, она проходит стадии преобразования, видоизменяется, но не исчезает. Самый простой пример, когда соприкасаются два предмета разной температуры, один холодный другой тёплый, то происходит отдача теповой энергии более холодному предмету.
Прочитать ещё 5 ответов
Как преобразуется кинетическая энергия?
Подбрасываем камень вверх, вначале кинетическая энергия маскимальна, далее она уменьшается, так как уменьшается скорость, но увеличивается высота, и увеличивается потенциальная энергия. В наивысшей точке кинетическая энергия равна 0, так как скорость 0, а потенциальная маскимальна, так как высота максимальна. Вот так и переходит.
Свет не имеет массы, откуда энергия?
Утверждение (свет не имеет массы) неточное. Не имеет массы (а правильнее – имеет нулевую массу) фотон – частица света. А луч света – это огромное количество фотонов, и он массу имеет (масса неаддитивна).
Фотон имеет нулевую массу, но не нулевую энергию. А почему вы решили, что энергией может обладать только то, что имеет массу? Это ниоткуда не следует.
Прочитать ещё 6 ответов
Как вычисляется механическая энергия?
Мои интересы: разнообразны, но можно выделить следующие: литература, история…
Для того, чтобы найти механическую энергию, нужно сначала определить кинетическую и потенциальную энергии, а затем сложить их, получим механическую энергию. Чтобы найти кинетическую энергию, нужно воспользоваться формулой: Ex= mv²/2, где: Ek – кинетическая энергия, (дж); m – масса тела (кГ); v – скорость (м/с). Чтобы определить потенциальную энергию, воспользуйтесь формулой: Ep = mgh, где: Ep – потенциальная энергия, (дж); g ускорение свободного падения (м2); m – масса тела (кГ); h высота центра масс тела над выбранным произвольно уровнем (м).
По Эйнштейну, чем ближе тело или частица к скорости света, тем огромнее становится его масса. И вот,в Большом адронном коллайдере, протоны и ионы, движутся почти со скоростью света, и что это значит?
Сусанна Казарян, США, Физик
Релятивистской массы нет в природе и, согласно релятивистской механике Эйнштейна, масса остаётся инвариантной и равной массе покоя всегда, независимо от скорости (недоверчивым сюда).
Темп роста энергии частицы (E) с ростом скорости β = v/c (в единицах скорости света c) получен мною здесь. Если тело обладало скоростью β₁ = 0,9 при энергии Е₁, то для достижения скорости β₂ = 0,9…999 (n девятoк после запятой), потребуется энергия E₂ = (3,16)ⁿ⁻¹⋅Е₁. Получается, что с каждой новой девяткой в величине скорости (β), энергия должна быть увеличена в 3,16 раз. Таким образом, неограниченный рост числа девяток (n) в численном значении скорости (β), приводит к неограниченному росту энергии.
Mаксимальная скорость зарегистрированного материального объекта (протона), ускоренного до околосветовых скоростей в космическом пространстве, равна β = 0,9…999 (всего 23 девятки), а соответствующая энергия, E ~ 10¹¹ ГэВ. Области в галактиках и механизмы ускорения до этих скоростей пока неизвестны. Максимальные энергии столкновения протонов, достигнутые на ускорителе БАК (LHC) в ЦЕРН, равны 1,3×10⁴ ГэВ, что в системе отсчёта неподвижной мишени соответствует энергии протона = 9×10⁷ ГэВ или скорости протона β = 0,999 999 999 999 9999 (16 девяток). В обоих случаях масса протона остаётся неизменной и равной массе покоя, 0.938 ГэВ.
Согласно релятивистской механике, со скоростью света (β = 1) могут лететь только безмассовые частицы (фотоны), но и у них есть недостаток − они не могут лететь медленнее.
Прочитать ещё 11 ответов
Источник

1. Камень, упав с некоторой высоты на Землю, оставляет на поверхности Земли вмятину. Во время падения он совершает работу по преодолению сопротивления воздуха, а после касания земли — работу по преодолению силы сопротивления почвы, поскольку обладает энергией. Если накачивать в закрытую пробкой банку воздух, то при некотором давлении воздуха пробка вылетит из банки, при этом воздух совершит работу по преодолению трения пробки о горло банки, благодаря тому, что воздух обладает энергией. Таким образом, тело может совершить работу, если оно обладает энергией. Энергию обозначают буквой ( E ). Единица работы — ( [E,] ) = 1 Дж.
При совершении работы изменяется состояние тела и изменяется его энергия. Изменение энергии равно совершенной работе: ( E=A ).
2. Потенциальной энергией называют энергию взаимодействия тел или частей тела, зависящую от их взаимного положения.
Поскольку тела взаимодействуют с Землёй, то они обладают потенциальной энергия взаимодействия с Землёй.
Если тело массой ( m ) падает с высоты ( h_1 ) до высоты ( h_2 ), то работа силы тяжести ( F_т ) на участке ( h=h_1-h_2 ) равна: ( A = F_тh = mgh = mg(h_1 — h_2) ) или ( A = mgh_1 — mgh_2 ) (рис. 48).
В полученной формуле ( mgh_1 ) характеризует начальное положение (состояние) тела, ( mgh_2 ) характеризует конечное положение (состояние) тела. Величина ( mgh_1=E_{п1} ) — потенциальная энергия тела в начальном состоянии; величина ( mgh_2=E_{п2} ) — потенциальная энергия тела в конечном состоянии.
Можно записать ( A=E_{п1}-E_{п2} ), или ( A=-(E_{п2}-E_{п1}) ), или ( A=-E_{п} ).
Таким образом, работа силы тяжести равна изменению потенциальной энергии тела. Знак «–» означает, что при движении тела вниз и соответственно при совершении силой тяжести положительной работы потенциальная энергия тела уменьшается. Если тело поднимается вверх, то работа силы тяжести отрицательна, а потенциальная энергия тела увеличивается.
Если тело находится на некоторой высоте ( h ) относительно поверхности Земли, то его потенциальная энергия в данном состоянии равна ( E_п=mgh ). Значение потенциальной энергии зависит от того, относительно какого уровня она отсчитывается. Уровень, на котором потенциальная энергия равна нулю, называют нулевым уровнем.
В отличие от кинетической энергии потенциальной энергией обладают покоящиеся тела. Поскольку потенциальная энергия — это энергия взаимодействия, то она относится не к одному телу, а к системе взаимодействующих тел. В данном случае эту систему составляют Земля и поднятое над ней тело.
3. Потенциальной энергией обладают упруго деформированные тела. Предположим, что левый конец пружины закреплён, а к правому её концу прикреплён груз. Если пружину сжать, сместив правый её конец на ( x_1 ), то в пружине возникнет сила упругости ( F_{упр1} ), направленная вправо (рис. 49).
Если теперь предоставить пружину самой себе, то её правый конец переместится, удлинение пружины будет равно ( x_2 ), а сила упругости ( F_{упр2} ).
Работа силы упругости равна
[ A=F_{ср}(x_1-x_2)=k/2(x_1+x_2)(x_1-x_2)=kx_1^2/2-kx_2^2/2 ]
( kx_1^2/2=E_{п1} ) — потенциальная энергия пружины в начальном состоянии, ( kx_2^2/2=E_{п2} ) — потенциальная энергия пружины во конечном состоянии. Работа силы упругости равна изменению потенциальной энергии пружины.
Можно записать ( A=E_{п1}-E_{п2} ), или ( A=-(E_{п2}-E_{п1}) ), или ( A=-E_{п} ).
Знак «–» показывает, что при растяжении и сжатии пружины сила упругости совершает отрицательную работу, потенциальная энергия пружины увеличивается, а при движении пружины к положению равновесия сила упругости совершает положительную работа, а потенциальная энергия уменьшается.
Если пружина деформирована и её витки смещены относительно положения равновесия на расстояние ( x ), то потенциальная энергия пружины в данном состоянии равна ( E_п=kx^2/2 ).
4. Движущиеся тела так же могут совершить работу. Например, движущийся поршень сжимает находящийся в цилиндре газ, движущийся снаряд пробивает мишень и т.п. Следовательно, движущиеся тела обладают энергией. Энергия, которой обладает движущееся тело, называется кинетической энергией. Кинетическая энергия ( E_к ) зависит от массы тела и его скорости ( E_к=mv^2/2 ). Это следует из преобразования формулы работы.
Работа ( A=FS ). Сила ( F=ma ). Подставив это выражение в формулу работы, получим ( A=maS ). Так как ( 2aS=v^2_2-v^2_1 ), то ( A=m(v^2_2-v^2_1)/2 ) или ( A=mv^2_2/2-mv^2_1/2 ), где ( mv^2_1/2=E_{к1} ) — кинетическая энергия тела в первом состоянии, ( mv^2_2/2=E_{к2} ) — кинетическая энергия тела во втором состоянии. Таким образом, работа силы равна изменению кинетической энергии тела: ( A=E_{к2}-E_{к1} ), или ( A=E_к ). Это утверждение — теорема о кинетической энергии.
Если сила совершает положительную работу, то кинетическая энергия тела увеличивается, если работа силы отрицательная, то кинетическая энергия тела уменьшается.
5. Полная механическая энергия ( E ) тела — физическая величина, равная сумме его потенциальной ( E_п ) и кинетической ( E_п ) энергии: ( E=E_п+E_к ).
Пусть тело падает вертикально вниз и в точке А находится на высоте ( h_1 ) относительно поверхности Земли и имеет скорость ( v_1 ) (рис. 50). В точке В высота тела ( h_2 ) и скорость ( v_2 ) Соответственно в точке А тело обладает потенциальной энергией ( E_{п1} ) и кинетической энергией ( E_{к1} ), а в точке В — потенциальной энергией ( E_{п2} ) и кинетической энергией ( E_{к2} ).
При перемещении тела из точки А в точку В сила тяжести совершает работу, равную А. Как было показано, ( A=-(E_{п2}-E_{п1}) ), а также ( A=E_{к2}-E_{к1} ). Приравняв правые части этих равенств, получаем: ( -(E_{п2}-E_{п1})=E_{к2}-E_{к1} ), откуда ( E_{к1}+E_{п1}=E_{п2}+E_{к2} ) или ( E_1=E_2 ).
Это равенство выражает закон сохранения механической энергии: полная механическая энергия замкнутой системы тел, между которыми действуют консервативные силы (силы тяготения или упругости) сохраняется.
В реальных системах действуют силы трения, которые не являются консервативными, поэтому в таких системах полная механическая энергия не сохраняется, она превращается во внутреннюю энергию.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Два тела находятся на одной и той же высоте над поверхностью Земли. Масса одного тела ( m_1 ) в три раза больше массы другого тела ( m_2 ). Относительно поверхности Земли потенциальная энергия
1) первого тела в 3 раза больше потенциальной энергии второго тела
2) второго тела в 3 раза больше потенциальной энергии первого тела
3) первого тела в 9 раз больше потенциальной энергии второго тела
4) второго тела в 9 раз больше потенциальной энергии первого тела
2. Сравните потенциальную энергию мяча на полюсе ( E_п ) Земли и на широте Москвы ( E_м ), если он находится на одинаковой высоте относительно поверхности Земли.
1) ( E_п=E_м )
2) ( E_п>E_м )
3) ( E_п<E_м )
4) ( E_пgeq E_м )
3. Тело брошено вертикально вверх. Его потенциальная энергия
1) одинакова в любые моменты движения тела
2) максимальна в момент начала движения
3) максимальна в верхней точке траектории
4) минимальна в верхней точке траектории
4. Как изменится потенциальная энергия пружины, если её удлинение уменьшить в 4 раза?
1) увеличится в 4 раза
2) увеличится в 16 раз
3) уменьшится в 4 раза
4) уменьшится в 16 раз
5. Лежащее на столе высотой 1 м яблоко массой 150 г подняли относительно стола на 10 см. Чему стала равной потенциальная энергия яблока относительно пола?
1) 0,15 Дж
2) 0,165 Дж
3) 1,5 Дж
4) 1,65 Дж
6. Скорость движущегося тела уменьшилась в 4 раза. При этом его кинетическая энергия
1) увеличилась в 16 раз
2) уменьшилась в 16 раз
3) увеличилась в 4 раза
4) уменьшилась в 4 раза
7. Два тела движутся с одинаковыми скоростями. Масса второго тела в 3 раза больше массы первого. При этом кинетическая энергия второго тела
1) больше в 9 раз
2) меньше в 9 раз
3) больше в 3 раза
4) меньше в 3 раза
8. Тело падает на пол с поверхности демонстрационного стола учителя. (Сопротивление воздуха не учитывать.) Кинетическая энергия тела
1) минимальна в момент достижения поверхности пола
2) минимальна в момент начала движения
3) одинакова в любые моменты движения тела
4) максимальна в момент начала движения
9. Книга, упавшая со стола на пол, обладала в момент касания пола кинетической энергией 2,4 Дж. Высота стола 1,2 м. Чему равна масса книги? Сопротивлением воздуха пренебречь.
1) 0,2 кг
2) 0,288 кг
3) 2,0 кг
4) 2,28 кг
10. С какой скоростью следует бросить тело массой 200 г с поверхности Земли вертикально вверх, чтобы его потенциальная энергия в наивысшей точке движения была равна 0,9 Дж? Сопротивлением воздуха пренебречь. Потенциальную энергию тела отсчитывать от поверхности земли.
1) 0,9 м/с
2) 3,0 м/с
3) 4,5 м/с
4) 9,0 м/с
11. Установите соответствие между физической величиной (левый столбец) и формулой, по которой она вычисляется (правый столбец). В ответе запишите подряд номера выбранных ответов
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Потенциальная энергия взаимодействия тела с Землёй
Б. Кинетическая энергия
B. Потенциальная энергия упругой деформации
ХАРАКТЕР ИЗМЕНЕНИЯ ЭНЕРГИИ
1) ( E=mv^2/2 )
2) ( E=kx^2/2 )
3) ( E=mgh )
12. Мяч бросили вертикально вверх. Установите соответствие между энергией мяча (левый столбец) и характером её изменения (правый столбец) при растяжении пружины динамометра. В ответе запишите подряд номера выбранных ответов.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Потенциальная энергия
Б. Кинетическая энергия
B. Полная механическая энергия
ХАРАКТЕР ИЗМЕНЕНИЯ ЭНЕРГИИ
1) Уменьшается
2) Увеличивается
3) Не изменяется
Часть 2
13. Пуля массой 10 г, движущаяся со скоростью 700 м/с, пробила доску толщиной 2,5 см и при выходе из доски имела скорость 300 м/с. Определить среднюю силу сопротивления, воздействующую на пулю в доске.
Ответы
Потенциальная и кинетическая энергия. Закон сохранения механической энергии
3.3 (65%) 12 votes
Источник
